Some thoughts on the role of Bayesianism in the age of Modern AI
It works because it works.
TLDR: Bayesian methods have undeniable value, e.g. in data analysis, but they play a peripheral role in “Modern AI” (i.e. deep learning), which prioritises scalable, empirical approaches over theoretical grounding—a trend that is unlikely to change.
Researchers across fields (including NLP!) are experiencing something of an existential crisis following the rapid rise of (large) language models (LMs).
Earlier this month, I had the pleasure to attend a week-long therapy session seminar on “Rethinking the Role of Bayesianism in the Age of Modern AI”.1 The event provided a great platform for ideas, debates, and reflections on where Bayesian methods stand and what their role might be in the fast-evolving AI field. This post is an attempt to write down some of my personal thoughts and feelings on the topic.
What is Modern AI?
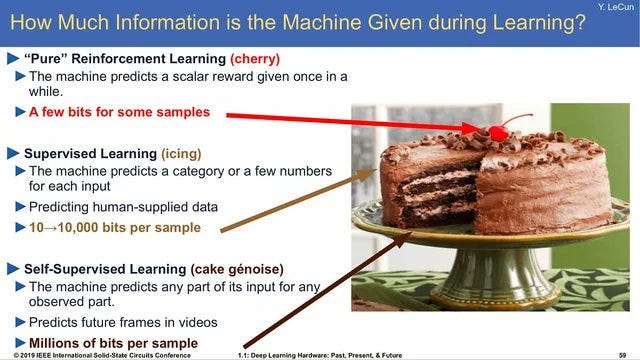
The workshop, perhaps intentionally, did not define what “Modern AI” is. I personally equate it with “large models that have been made to do useful things” and this is the definition I’m adopting in this post. A great analogy for breaking down the core components of Modern AI is the LeCun cake:
Unsupervised Learning: cake genoise
Supervised Learning: icing
Reinforcement Learning: cherry on top
At the workshop, there was a broad consensus that Bayes is not needed for the base of the cake, i.e. for self-supervised learning. Could Bayesian methods be useful for improving the other parts of the cake? Let’s explore this by considering their key strengths.
The traditional strengths of Bayesian methods
Typically, Bayesian methods are used for two main reasons: (1) Uncertainty quantification (UQ) and (2) Preventing overfitting.2
Uncertainty quantification
Parameter uncertainty, which is what Bayesian methods traditionally aim to capture, is not particularly meaningful for the large models that the cake is made out of. Predictive uncertainty — the uncertainty around the model’s outputs, is certainly valuable, provided it has desirable properties, such as calibration.
In theory, Bayesian methods provide us a principled pathway to predictive uncertainty by propagating uncertainty from the chosen priors through to posterior distributions. In practice, however, we have
Poor priors. Beyond some debates if these should be set in parameter or function space, the Bayesian ML community tends to overlook the critical importance of prior specification. Priors are usually selected for mathematical convenience, incorporating neither subjective beliefs nor expert knowledge. If we don’t have meaningful priors, why should we expect them to yield meaningful uncertainties?
Questionable posteriors. Exact posterior inference is impossible. Approximate inference at such a large scale is very expensive, and the quality of the resulting posteriors is hard to assess. More crucially, desirable properties like calibration—a key goal of uncertainty quantification—rarely hold (in theory and in practice).
Massive cost. The entire procedure introduces huge computational and memory overheads both during training and at inference time, and generally results in a worse performance.
If the goal is predictive uncertainty, why are we burdening ourselves with priors and posteriors that offer little practical benefit? There are more direct and efficient methods—like conformal prediction—that provide well-calibrated predictive uncertainties (at least in theory) and introduce less complexities.
Preventing overfitting
Empirically, overfitting is not a significant concern for the quality of the cake. Intuitively, this is because of the huge amount of data we train on. During the workshop, one attendee presented a compelling mathematical argument to show that Bayesian methods offer no notable advantages when training for one or very few epochs, which is the regime for large models.
In scenarios where overfitting does become a concern—e.g. if we have to train for many epochs— there are numerous simpler regularisation methods, such as data augmentation, dropout etc., that have been found to work well in practice without requiring the complexities of Bayesian inference.
I can already hear “but all of these things work because they are (implicitly) Bayesian”…
Retrofitting Bayesianism
There's a tendency within the Bayesian ML community to retrospectively attribute the success of various methods to Bayesian principles. Whilst post-hoc explanations can provide valuable insights, they don’t necessarily push the field forward. This might be an unpopular opinion, but I view these attempts to reinterpret every successful method as inherently Bayesian as a form of intellectual overfitting.
Conclusions
Whilst Bayesian methods certainly have their place in more “classical” settings (e.g. data analysis, specific applications), my current view is that their role in the development of “Modern AI”, as defined in this post, is limited and is likely to remain such. I am not dogmatic and will change my mind once a Bayesian (or Bayesian-inspired, but not retrofitted!) method can consistently produce a substantially better cake. Until then the traditional recipe is the best we’ve got:

Jokes aside, kudos to the organisers (especially Vincent Fortuin) for putting together such a fantastic event!
Some dogmatic Bayesians might add a third reason, namely because “it's the principled thing to do”.